2022. 12. 6. 18:25ㆍMetallurgical Processing/기본이론
pH와 pOH 계산법에서 알 수 있듯이, pH를 결정하는 것은 수소이온의 농도([H+]) 혹은 수산화이온의 농도([OH-])입니다. 따라서, 흔히 우리가 알고있는 산, 염기의 화학식을 본다면 수소이온이나 수산화이온을 포함하고 있습니다. 대표적으로 황산(H2SO4), 질산(HNO3), 아세트산(CH3COOH) 등이 있습니다. 이들은 물 등 용매에 용해되어 이들 이온을 내놓고 용액을 산성화 혹은 알칼리화 시킵니다.
하지만, 어떤 특정 산이 동일한 양의 수소이온을 포함하고 있다해서, 이들이 동일한 산도 혹은 pH를 나타내는 것은 아닙니다. 각 산은 크게 강산 혹은 약산으로 나뉠 수 있는데, 이는 산의 해리(acid dissociation)과 관련이 있습니다.

산의 해리: Acid dissociation
위에서 말씀드린것 처럼, 산의 강도는 수용액 내에서 쉽게 해리될 수 있는지에 따라서 결정됩니다. 즉, 산이 물에 섞여 반응을 할 때 생성되는 이온 혹은 해리 될 때, 이들이 100%에 가깝게 해리가 된다면 강산, 거의 해리되지 않는다면 약산입니다. 이 해리의 용이성을 나타내는 상수를 산 해리 상수(acid dissociation constant)라 하며, Ka 혹은 pKa로 나타냅니다. (각각의 산은 고유한 산 해리 강도를 가집니다.)


Ka: 산 해리 상수
pKa: 산 해리 상수의 로그스케일로, 산 간의 강약을 비교하기 위해 사용되기도 함
HA: 임의의 산(H-A)
아래의 표는 강산, 약산을 나누는 산 해리 상수와 pKa를 나타낸 것입니다.
Table 1. Acids, Ka, and pKa
| Acid | Ka | pKa |
| Very strong acid | > 0.1 | < 1 |
| Fairly strong acid | 10-3 - 0.1 | 1 - 3 |
| Weak acid | 10-5 - 10-3 | 3 - 5 |
| Very weak acid | 10-15 - 10-5 | 5 - 15 |
| Extremely weak acid | < 10-15 | > 15 |
산의 해리와 pH 계산
강산과 약산의 차이는 해리의 정도이고 결국에는 pH 값에 영향을 미칩니다. 아래는 산의 해리와 이에 따른 pH 값을 계산하는 방법입니다.
(1) H2SO4의 해리
황산(H2SO4)은 강산에 속합니다. 황산은 총 2단계에 걸쳐서 해리되며, 해리될 때 각기 다른 해리 상수로 해리됩니다. 예시로 0.05M H2SO4의 해리를 보겠습니다. 아래는 첫번째 해리입니다. 황산의 첫번째 해리는 적당한 농도 범위에서 거의 100% 완벽하게 이루어집니다 (해리 상수가 매우 큼).

다음으로 두번째 해리입니다. 이 때, HSO4-의 초기 농도는 완전해리 된 H2SO4의 농도와 동일하고, 이미 수용액 중에 해리된 수소이온 또한 있으므로 이를 고려하여 방정식을 세워야 합니다.

아래의 Initial-Change-Equilibrium (ICE) 표를 이용하여, 방정식 (1.2.1)을 세우는데 활용할 수 있습니다.
| [ICE Table] | HSO4- | H+ | SO42- |
| Initial | 0.05 | 0.05 | 0 |
| Change | -x | +x | +x |
| Equilibrium | 0.05-x | 0.05+x | +x |


따라서 0.05M H2SO4의 pH는 계산법에 따라, -log10[H+]≒-log100.0585=1.23입니다.
(2) H3PO4의 해리
인산(H3PO4)은 약산에 속합니다. 인산은 총 3 단계에 걸쳐서 해리되는데, 이 또한 해리될 때 각기 다른 해리 상수로 해리됩니다. 예시로, 5M H3PO4의 해리를 보겠습니다. 아래는 첫번째 해리입니다.

위의 반응식을 통해, 해리된 이온의 농도를 구하기 위한 방정식을 세우면 아래 식 2.1.1*과 같습니다.
*단, 해리되는 양 x가 전체의 5%를 넘지 않는다고 가정
| [ICE Table] | H3PO4 | H+ | H2PO4- |
| Initial | 5 | 0 | 0 |
| Change | -x | +x | +x |
| Equilibrium | 5-x | +x | +x |


**0.19M은 해리된 이온의 양입니다. 즉, 인산은 전체 5.0M의 4% 정도만이 해리된 것입니다.
이제 두번째 해리입니다. 이 때, H2PO4-의 초기 농도는 위의 x(0.19M)와 동일하고, 이미 수용액 중에 해리된 수소이온(0.19M)이 있으므로 이를 고려하여 방정식을 세워야 합니다.

이전과 같은 방법으로 방정식을 세우면 아래 식 2.2.1가 되는데, 이 때 y의 값은 0.19보다 훨씬 작으므로 이차 방정식을 통해 적절한 답을 찾으면 됩니다.
| [ICE Table] | H2PO4- | H+ | HPO42- |
| Initial | 0.19 | 0.19 | 0 |
| Change | -y | +y | +y |
| Equilibrium | 0.19-y | 0.19+y | +y |
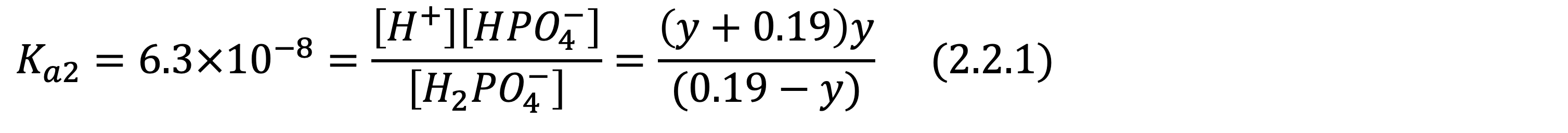
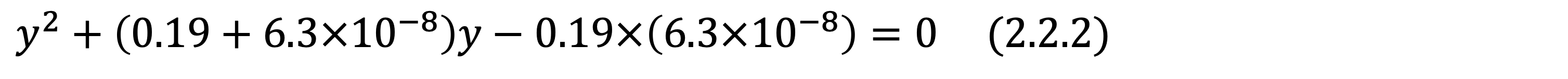

마지막으로 세번째 해리입니다. 위와 같은 방식으로 구하면 됩니다.

| [ICE Table] | HPO42- | H+ | PO43- |
| Initial | 6.3X10-8 | 0.19 | 0 |
| Change | -z | +z | +z |
| Equilibrium | 6.3X10-8-z | 0.19+z | +z |
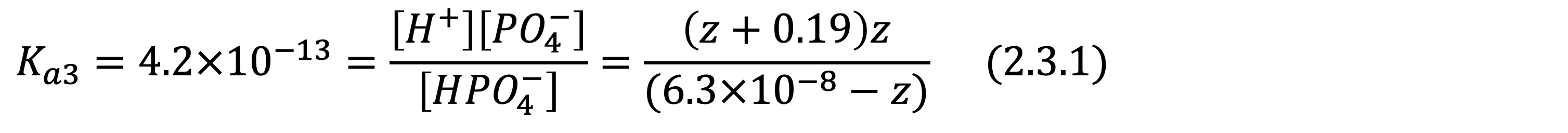
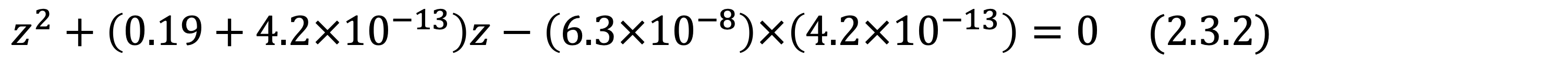

위의 인산의 해리 과정에서 보셨듯, 두번째 세번째 해리는 거의 일어나지 않으며 pH 미치는 영향은 미미합니다. 따라서 5M H3PO4의 pH는 계산법에 따라, -log10[H+]≒-log100.19=0.72입니다.
'Metallurgical Processing > 기본이론' 카테고리의 다른 글
| Oxidation Reduction (산화 환원) (0) | 2022.12.07 |
|---|---|
| Oxidation number(산화수) (0) | 2022.12.07 |
| Galvanic reaction(갈바닉 반응) (0) | 2022.10.31 |
| 입자의 반응 속도모델 (0) | 2022.06.20 |
| Arrhenius's equation(아레니우스 식) (0) | 2022.06.20 |
