2020. 7. 20. 00:53ㆍMineral Processing/Comminution (파분쇄공정)
장비의 전력소모에 대한 예측은 선광 플랜트의 설계 시 매우 중요한 요소 중 하나입니다. 일반적으로 설계과정에서 이를 구하기 위하여 채취된 샘플을 아래와 같이 대표적인 선광연구소에 위탁하는 경우가 많습니다.
˙SGS Lakefield(Societe Generale de Surveillance)
˙CSIRO(The Commonwealth Scientific and Industrial Research Organisation)
˙MINTEK
파분쇄이론: Theory of comminution
급광입자의 크기를 어느정도의 크기로 감소(Size reduction)시키기 위하여 필요한 에너지를 규명하기 위한 이론입니다. 파분쇄에 투입되는 에너지 중, 대부분의 에너지가 열, 소리 등으로 손실되며 실제로 파분쇄에 이용되는 에너지는 적습니다.

대표적으로, (1) Rittinger's Law와 Kick's Law 그리고 (2) Bond's Law가 있습니다. (이들은 흔히 Law라 불리나 이들 모두 가정(Hypothesis)을 전제로 한 모델임)
(1) Ritting's Law와 Kick's Law
1-1) Rittinger's Law
파분쇄에 소모되는 에너지는 새롭게 생성되어 늘어나는 입자의 면적에 비례한다는 가정을 둔 식입니다. 식 (1.1.5)로부터 입자의 구형도 Φ가 파분쇄 전후에 동일하다고 가정하고 나머지 앞의 계수들을 Rittinger 상수 KR로 놓았을 때, 아래와 같이 식 (1.1)로 표현할 수 있습니다.

E: 전력소모량 (kWh/ton)
KR: Rittinger 상수
F80: 급광입자의 80% 통과 누적 입도
P80: 분쇄산물입자의 80% 통과 누적 입도
[참고1] 기본식 도출 과정
파분쇄는 에너지를 가하여 더 작은 크기의 입자를 형성하는 것이며, 이 때 파분쇄 대상에 의하여 흡수된 에너지(파분쇄에 직접 사용된 에너지)가 입자의 표면적증가에 비례할 경우 아래와 같이 표현할 수 있습니다.

Wn: 파분쇄 대상의 단위 질량 당 흡수된 에너지
es: 표면에너지
Awb: 파분쇄 산물 입자의 단위 질량 당 표면적
Awa: 파분쇄 대상 입자의 단위 질량 당 표면적
ηc: Comminution Efficiency
이 때, 장비를 운전함으로써 손실되는 에너지를 ηm이라 하였을 때 파분쇄에 사용되는 전체 에너지는 아래와 같이 표현할 수 있습니다.
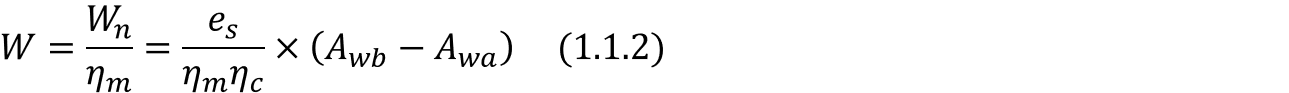
어느 한 입자에 대하여, 구형도를 아래와 같이 표현하고

Φs: 입자의 구형도 [참고3]
vp: 입자의 부피
Dp: 입자의 지름
sp: 입자의 표면적
이런 균일한 입자들이 질량 m만큼 모여있을 때, 이 입자들의 개수를 N이라 하면,

N: 벌크 내 입자의 개수
m: 벌크 질량
ρ: 입자의 밀도
라 할 수 있으며, 이 때 식 (1.1.2.1)과 식 (1.1.2.2)를 이용하여, 입자들의 전면적 A를 아래 식 (1.1.2.3)과 같이 표현할 수 있습니다.
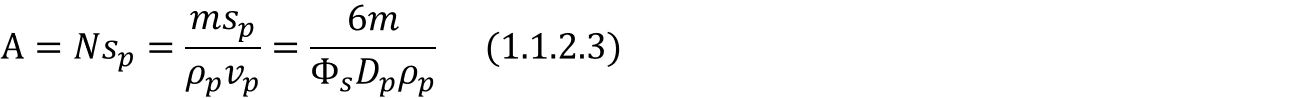
이 때, 각각의 입자는 밀도는 같으나 크기가 다를 수 있으므로 각 입자들의 무게를 xi(1≤i≤n)라 하였을 때, 실제 입자의 전면적 Aw를 아래 식 (1.1.2.4)와 같이 표현할 수 있습니다.
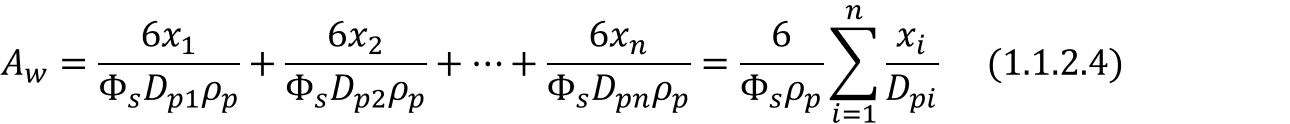
이를 간단하게 평균입자의 지름으로 근사시켰을 때,

이를 식 (1.1.2)에 대입하면, 식 (1.1.3)과 같이 변형시킬 수 있습니다.

단위 시간당 급광되는 광석량을 ṁ이라하였을 때, 요구되는 전력량 P에 대해서 식 (1.1.4) 혹은 식 (1.1.5)로 나타낼 수 있습니다.
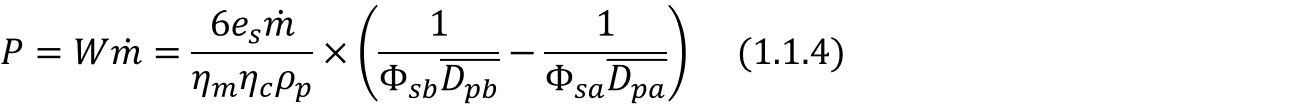
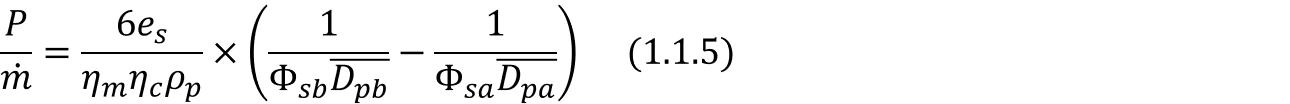
1-2) Kick's Law
파분쇄에 소모되는 에너지는 급광입자와 파분쇄산물 입자의 크기의 비와 비례 즉, 부피감소에 비례한다는 가정을 둔 식입니다.

E: 전력소모량 (kWh/ton)
KK: Kick 상수
F80: 급광입자의 80% 통과 누적 입도
P80: 분쇄산물입자의 80% 통과 누적 입도
1-3) 경험관계식: Rittinger's Law와 Kick's Law

식 (1.3)은 n=1일 때는 Kick's Law를, n=2일 때는 Rittinger's Law를 표현하는 식입니다. (계수 K는 실험을 통해 구해짐)
(2) Bond's Law and Work Index (1952)*
*The Third Theory of Comminution, AIME Trans., Vol. 193, p. 484, 1952. Also in Mining Engineering, May 1952
Rittinger 그리고 Kick's Law에 비하여 요구되는 전력량을 더욱 현실적으로 추정할 수 있도록 고안된 것으로, 식 (1.3)에서 n=1.5일 때에 해당합니다. (Fred C. Bond가 이 때 처음으로 일지수 - Work Index에 대한 개념을 도입하였음)

E: 전력소모량 (kWh/ton)
F80: 급광입자의 80% 통과 누적 입도
P80: 분쇄산물입자의 80% 통과 누적 입도
Wi: Bond's Work Index. 광석의 단단한 정도(경도)를 나타내며 즉, 높은 수치일수록 파분쇄하기가 어려워짐 (kWh/ton)
혹은, 실제 운전을 통해 얻은 데이터와 식 (2.1)을 이용함으로써 역으로 Work Index를 계산할 수도 있습니다. [참고2]
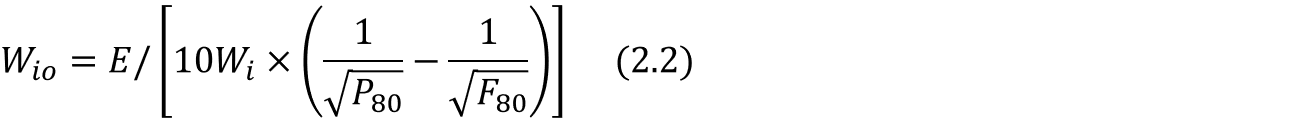
Wio: Operational Work Index
[참고2] Bond's Work Index
Bond's Work Index by Ore Type은 흔한 광물들에 대한 Work Index를 나타낸 것입니다. Work Index가 클수록 광석을 파분쇄하기 어려워집니다.
Table 1. Bond's Work Index by Ore Type
| Material | Specific Gravity | Work Index, Wi |
| Bauxite | 2.20 | 8.78 |
| Coal | 1.40 | 13.00 |
| Granite | 2.66 | 15.13 |
| Gravel | 2.66 | 16.06 |
| Gypsum Rock | 2.69 | 6.73 |
| Hematite | 3.53 | 12.84 |
| Limestone | 2.66 | 12.74 |
| Phosphate Rock | 2.74 | 9.92 |
| Quartz | 2.65 | 13.57 |
| Shale | 2.63 | 15.83 |
| Slate | 2.57 | 14.30 |
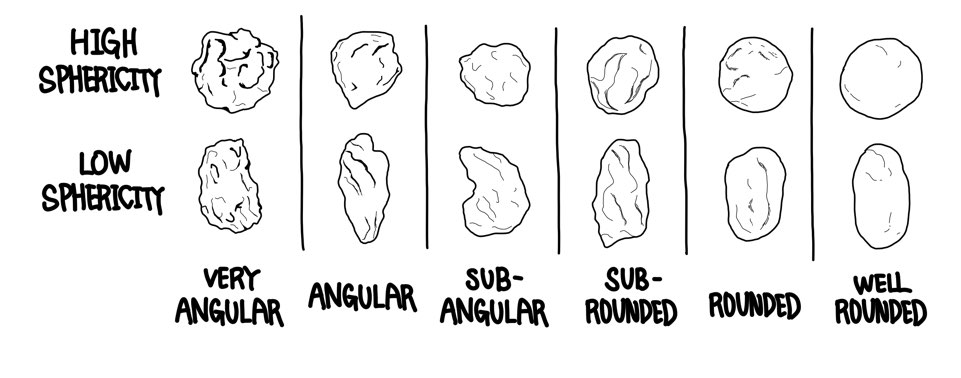
[참고3] Sphericity와 Roundness
구형도(Sphericity)는 입자가 구에 얼마나 가까운지를 나타내는 것인 반면 원마도(Roundness)는 각 모서리가 마모되어 둥근 정도를 의미합니다.
'Mineral Processing > Comminution (파분쇄공정)' 카테고리의 다른 글
| 분쇄공정 - 회전밀의 회전속도와 분쇄매체의 움직임 (0) | 2020.07.23 |
|---|---|
| 분쇄공정 - 회전밀의 유형(Type of Tumbling Mill) (0) | 2020.07.21 |
| 파분쇄공정 - 파분쇄 및 각 공정별 대표장비 (0) | 2020.07.17 |
| 파분쇄공정 - 단체분리(Liberation) (0) | 2020.07.14 |
| 분쇄공정 - 회전밀 장치 구조(Lubrication System) (0) | 2020.07.10 |
